Reconfigurable Circuits

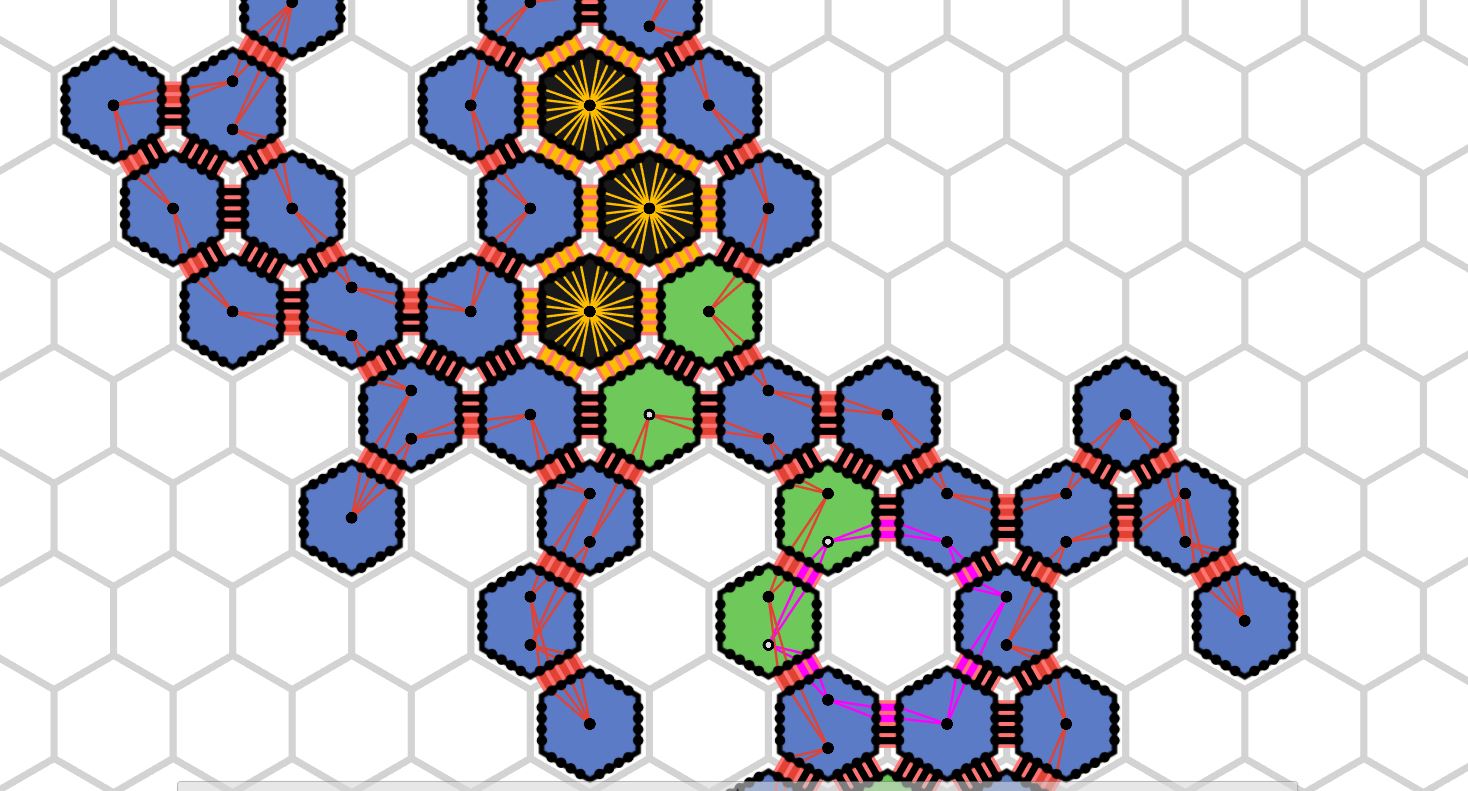
In the basic amoebot model, information can only be transmitted between neighboring amoebots. This means that it may take \(\Theta(n)\) rounds for a message to spread through a structure of \(n\) amoebots. The reconfigurable circuits extension allows the amoebots to establish so-called circuits, which are structures spanning an arbitrary number of amoebots allowing the instant transmission of signals to all amoebots that are part of the circuit. The significantly faster communication enables the amoebots to tackle problems in new ways and decrease the number of rounds required to solve problems.

Model Description

The following description is taken and edited from Coordinating Amoebots via Reconfigurable Circuits by Feldmann, Padalkin, Scheideler and Dolev (Springer International Publishing, 2021) and The Structural Power of Reconfigurable Circuits in the Amoebot Model by Padalkin, Scheideler and Warner (Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2022):

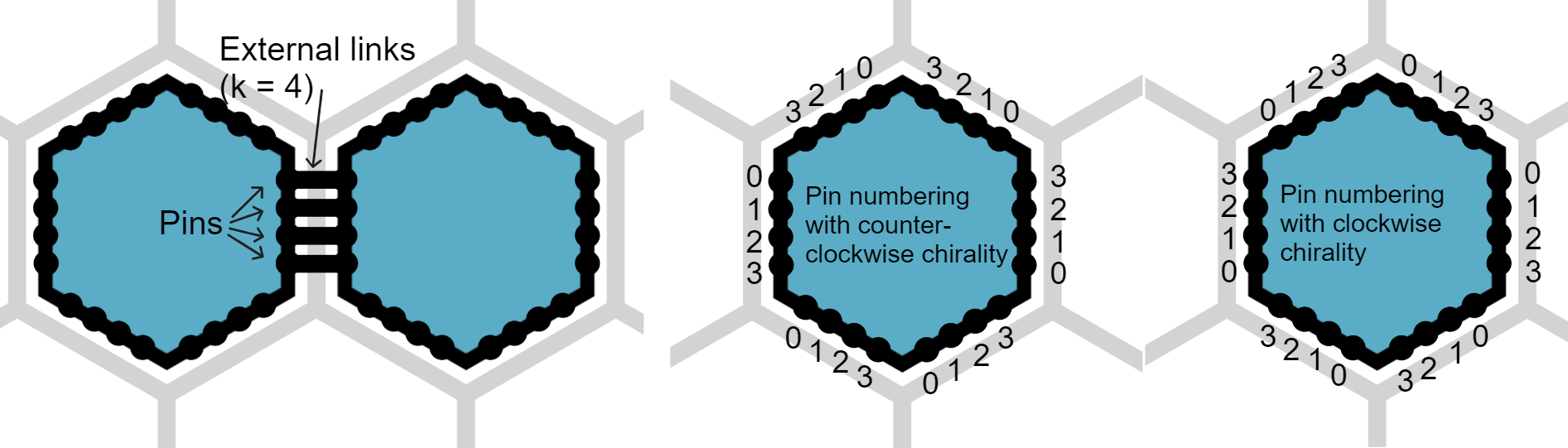
In our reconfigurable circuit extension, each edge between two neighboring amoebots \(u\) and \(v\) is replaced by \(k\) edges called external links with endpoints called pins, for some constant \(k \geq 1\) that is the same for all amoebots. For each of these links, one pin is owned by \(u\) while the other pin is owned by \(v\). We assume that the \(k\) pins on the side of \(u\) resp. \(v\) are consecutively numbered from \(0\) to \(k-1\), and there are two possible ways by which these pins are matched (i.e., belong to the same link). If \(u\) and \(v\) have the same chirality, pin \(i\) of \(u\) is matched with pin \(k - i - 1\) of \(v\), and if \(u\) and \(v\) have different chiralities, pin \(i\) of \(u\) is matched with pin \(i\) of \(v\).

Each amoebot \(u\) partitions its pin set \(P(u)\) into a collection \(\mathcal{Q}(u)\) of pairwise disjoint subsets such that the union equals the pin set, i.e., \(P(u) = \bigcup_{Q \in \mathcal{Q}(u)} Q\). We call \(\mathcal{Q}(u)\) the pin configuration of \(u\) and \(Q \in \mathcal{Q}(u)\) a partition set of \(u\). Let \(\mathcal{Q} = \bigcup_{u \in S} \mathcal{Q}(u)\) be the collection of all partition sets in the structure. Two partition sets are connected iff there is at least one external link between those sets. Let \(L\) be the set of all connections between the partition sets in the structure. Then, we call \(H = (\mathcal{Q}, L)\) the pin configuration of the structure and any connected component \(C\) of \(H\) a circuit. Note that if each partition set of \(\mathcal{Q}\) is a singleton, i.e., a set with exactly one element, then every circuit of \(H\) just connects two neighboring amoebots. However, an external link between the neighboring amoebots \(u\) and \(v\) can only be maintained as long as both, \(u\) and \(v\) occupy the incident nodes. Whenever two amoebots disconnect, the corresponding external links and their pins are removed from the structure. An amoebot is part of a circuit iff the circuit contains at least one of its partition sets. A priori, an amoebot \(u\) may not know whether two of its partition sets belong to the same circuit or not since initially it only knows \(\mathcal{Q}(u)\).

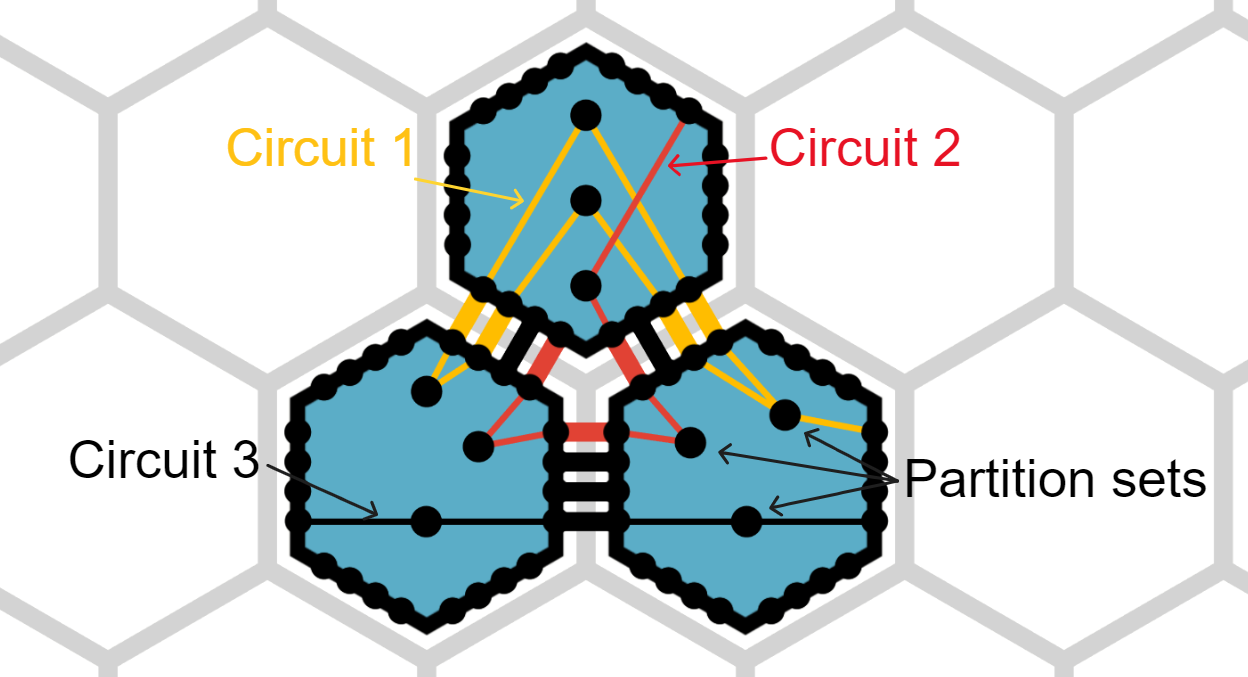The figure above shows a pin configuration with three non-trivial circuits. The big black circles inside the amoebots represent the non-empty and non-singleton partition sets. Each partition set contains all pins that are connected to its circle by the thin internal connection lines. The thicker lines between the amoebots represent the external connections. Note that there are more than three circuits in the pin configuration, but many of them are trivial (i.e., they only connect two pins). Also note that the top amoebot does not know that some of its partition sets belong to the same circuit.

Each amoebot \(u\) can send a primitive signal (a beep) via any of its partition sets \(Q \in \mathcal{Q}(u)\) that is received by all partition sets of the circuit containing \(Q\) at the beginning of the next round. The amoebots are able to distinguish between beeps arriving at different partition sets. More specifically, an amoebot receives a beep at partition set \(Q\) if at least one amoebot sends a beep on the circuit belonging to \(Q\), but the amoebots neither know the origin of the signal nor the number of origins. Note that beeps are enough to send whole messages over time, especially between adjacent amoebots. We modify an activation of an amoebot as follows. As a function of its previous state and the beeps received in the previous round, each amoebot may perform a movement, update its state, reconfigure its pin configuration, and activate an arbitrary number of its partition sets. The beeps are propagated on the updated pin configurations.

Messages

The simulator implements a feature addressing the fact that a sequence of beeps can be used to transmit arbitrary messages of constant size. In addition to sending simple beeps, it allows sending custom structs via circuits in a single round. This feature is added to avoid having to manually encode and decode information in a binary format and transmitting it over several rounds. It should be easy to see that this is possible for any finite-size struct and allowing the transmission of such data in a single round does not change the complexity of any problem or algorithm. Please refer to the Model Reference page on pin configurations for more information on how the reconfigurable circuits extension is implemented and used in the simulator.

Beep Failures

An interesting avenue of research is examining the setting where the circuits may not be reliable. In this setting, there is a failure probability \(p\) specifying the chances of beeps or messages not being received. More precisely, in every round and for each partition set of an amoebot, the partition set fails to receive any incoming beeps or messages with probability \(p\). Even if the amoebot sends a beep or message on this partition set, it will not receive anything if a failure occurs on that partition set in this round. The simulator implements this feature by providing a beep failure probability setting in the configuration file and in the Settings Panel. Through this option, you can directly control the value of \(p\). Partition sets on which a beep failure occurs are marked with a red highlight instead of the gray highlight indicating that a beep or message was received.

Continue by reading about the second extension of the amoebot model, joint movements