Model Reference: Directions and Compasses

Amoebots in the amoebot model live on a two-dimensional plane that is organized by the equilateral triangular grid, as explained in the amoebot model reference. On this plane, there are infinitely many directions, but due to the triangular grid, a small set of directions is much more relevant for the amoebots than all other directions. This page explains what these directions are and how the amoebots perceive them in their local perspective.

Directions

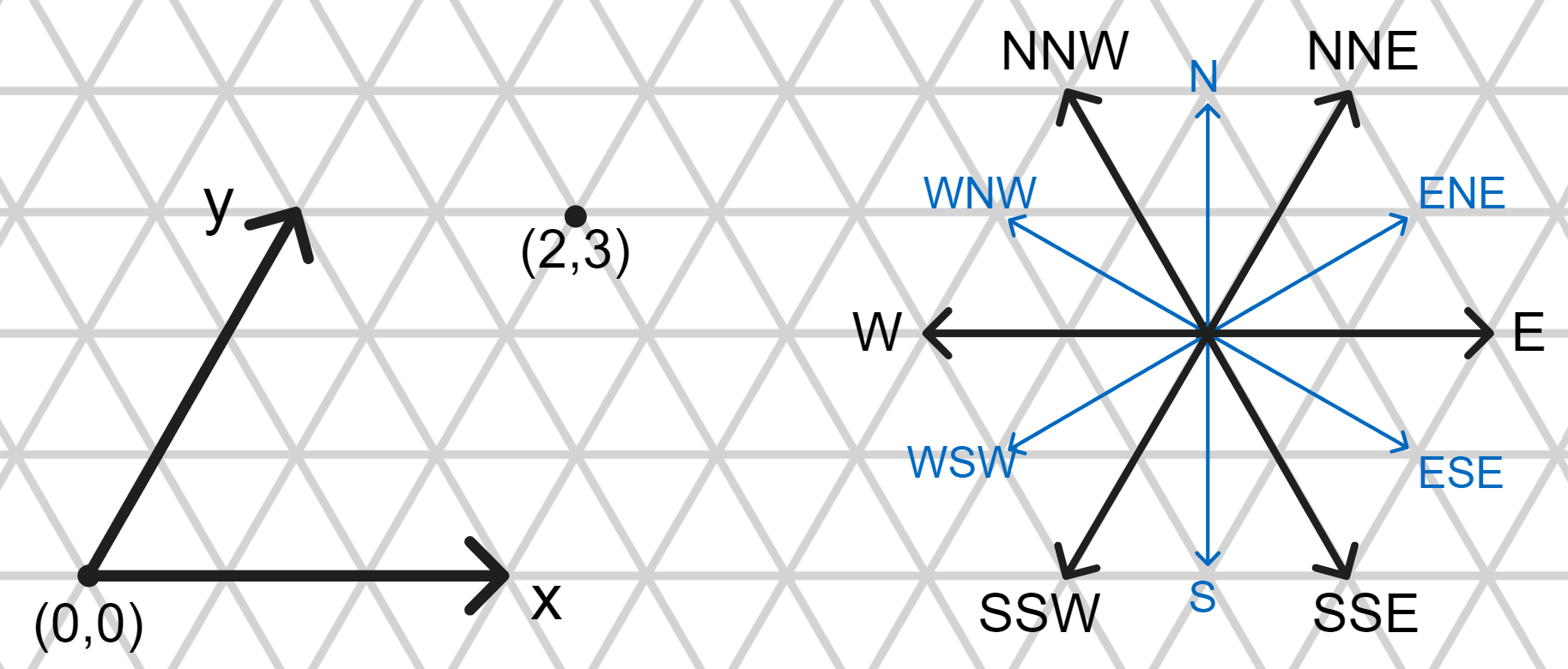
In the triangular grid graph, every node has six neighbors that are evenly spaced out at \(60^\circ\) angles around the node. Due to this structure, we have three axes, at \(60^\circ\) to each other, such that every edge in the grid graph is parallel to one of the axes. Each of the axes defines two directions in the plane. We orientate the grid such that one of the axes is horizontal and call the direction going to the right side East and the direction going to the left West. Accordingly, the four directions defined by the other two axes are called North-North East, North-North West, South-South West and South-South East. We call these six directions the primary or cardinal directions and abbreviate them with E, NNE, NNW, W, SSW, SSE, starting with East and going around in \(60^\circ\) steps in counter-clockwise direction. Using the same order, we identify the cardinal directions with the integers \(0,\ldots,5\). The cardinal directions are those directions in which the amoebots can perform movements and find their neighbors, because every (directed) edge of the grid graph points in a cardinal direction.

Additionally, we define a second set of directions by rotating the cardinal directions by \(30^\circ\). These secondary directions lie exactly between the cardinal directions and are named East-North East, North, West-North West, West-South West, South and East-South East, abbreviated ENE, N, WNW, WSW, S, ESE, and also identified by \(0,\ldots,5\) in that order. The secondary directions are useful for some algorithms because each secondary direction lies not only directly between two cardinal directions, it is also perpendicular to two of them and its axis runs through infinitely many nodes of the grid, which means that the secondary directions can be used to define certain amoebot structures.

We use the E-W axis and the NNE-SSW axis to define a global coordinate system, placing its origin with the coordinates \((0, 0)\) at some arbitrary node. However, the amoebots have no way of finding out their global coordinates unless they are given to them as parameters.

API Representation

In the simulator code, directions are represented by the Direction enum. It contains constants for all cardinal and secondary directions plus the special NONE value, which represents no direction. All Direction values can be converted to their integer representation using the ToInt extension method, the NONE value is represented by \(-1\). The static DirectionHelpers class provides various methods for working with directions, like rotating and reversing them or calculating the angle between two directions. Operations with the NONE value will result in NONE or \(-1\), depending on the return type.

Compass

Every amoebot has a local compass. The compass defines how the amoebot's local directions correspond to the global directions we defined above. This is done using the compass direction, which is the global cardinal direction that the amoebot believes to be East in its local view. All other directions are rotated together with the East direction in the local system. If an amoebot's compass direction is East (and its chirality matches the global orientation, see Chirality), its local directions match the global directions. In any other case, there is an offset between the local and global directions (and even different offsets if the chirality is inverted). For example, if an amoebot's compass direction is NNW, its local East direction will be the global NNW direction, and its local West direction will be SSE in the global view.

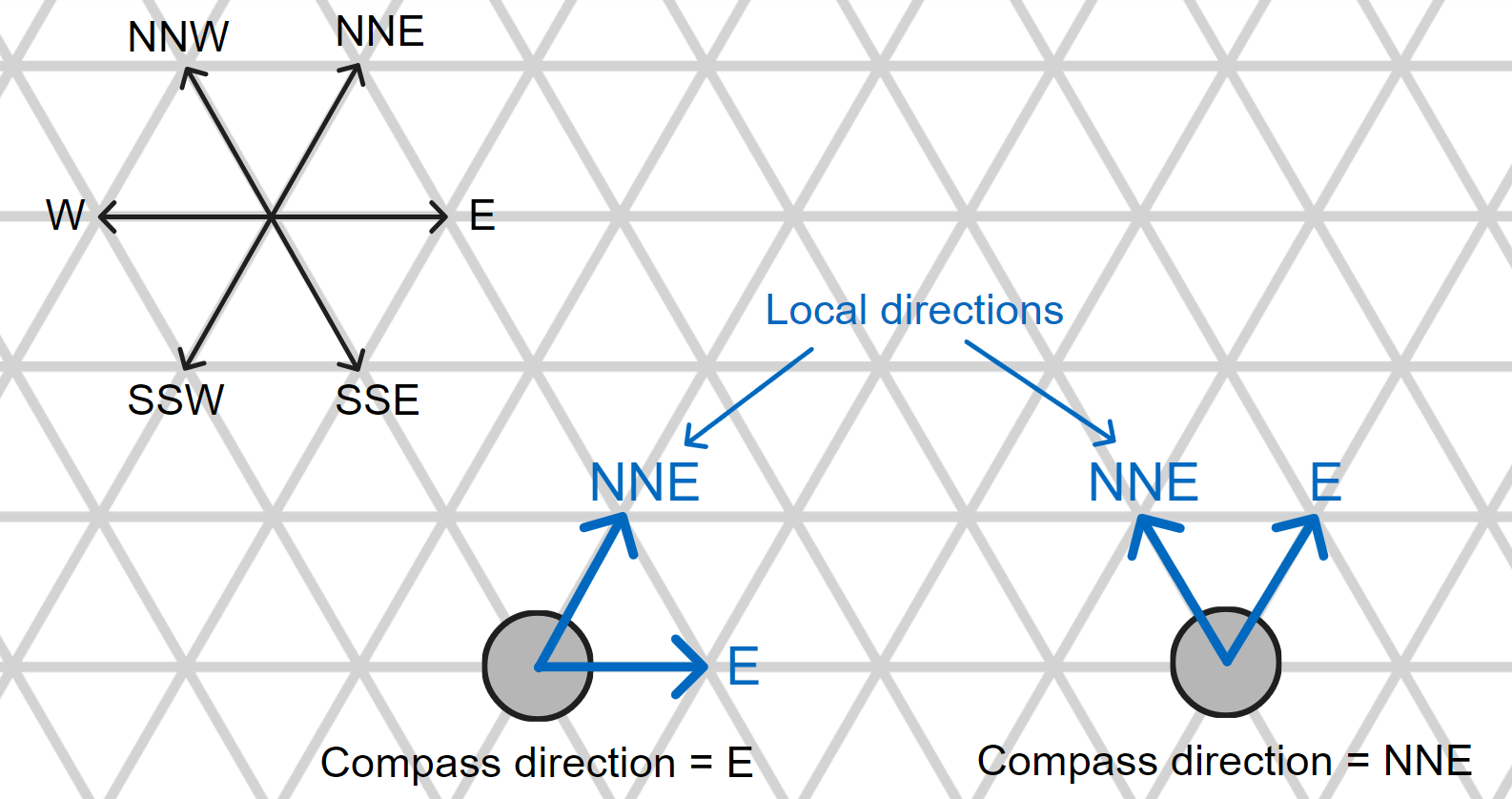
An amoebot does not know its compass direction and has no way to determine it.

Compass Alignment

Even though an amoebot can never find out its compass direction, there are ways for amoebots to agree on a common compass orientation using a compass alignment algorithm. For example, if two neighboring amoebots \(p\) and \(q\) have the same chirality, they can communicate their relative directions to each other: \(p\) tells \(q\) in which local direction \(q\) lies from \(p\)'s perspective and vice-versa. Due to the common chirality, this is enough information for both amoebots to know the relative offset between their compass directions. Using a coin toss to break the symmetry, the amoebots can decide which one of them changes its compass direction to match the other's. Note that the amoebots are not able to change their actual compass direction, but they can emulate such a change by treating directions as if they had an offset. The "Chirality & Compass Alignment" algorithm that is part of the simulator project demonstrates this technique after establishing a common chirality in the structure. Note that the algorithm relies on randomness due to the coin tosses, which means that it is not guaranteed to terminate. However, in practice, this generally does not cause any problems.

Setting the Compass Direction

The compass direction of an amoebot is set during the structure initialization in the Init Mode. It cannot be changed during the simulation, but the amoebot can emulate changing its compass. The default generation algorithm, which places the amoebots randomly but connected, has a parameter that defines the compass direction. If a cardinal direction is selected, all amoebots will have that direction as their compass direction. If "Random" is selected, the compass direction of each amoebot is chosen randomly from the six cardinal directions. For custom initialization algorithms, all API methods that place amoebots have a similar parameter. The compass direction can also be set manually in the UI while in Init Mode.